Finding The Domain Of A Function With A Square Root
Domain And Range Of Trigonometric Functions
Look at the graph of the sine function and cosine function. Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.
The domain and range of a trigonometry function are given as follows
Domain: The domain of the functions is the set R.
Range: The range of the functions is
Finding The Domain Of A Function Defined By An Equation
In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a holding area that contains raw materials for a function machine and the range as another holding area for the machines products ).
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket \). We will discuss interval notation in greater detail later.
Before we begin, let us review the conventions of interval notation:
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- Parentheses, \ or \\), are used to signify that an endpoint is not included, called exclusive.
- Brackets, \, are used to indicate that an endpoint is included, called inclusive.
Don’t Miss: How To See Who Owns A Domain
Finding Domain Of A Function With A Square Root In The Numerator And Denominator
From Rule 6 we know that a function of the form f=\sqrt} is defined when g\geq0 and h> 0.
Example:
f=\sqrt}
Solution:
For f to be defined,
3-x\neq 0
Now we have to find the set of values of x so that
\frac\geq 0
Here we can not directly say x-2> 0 because we do not know the sign of 3-x.
To overcome this problem we will make the denominator +ve by multiplying the numerator and denominator by
i.e., \frac}\geq 0
i.e., \geq 0
Next we have to find the values of x so that \geq 0
Now see the table given below:
| Value of x | \geq 0 satisfied or not | ||
|---|---|---|---|
| x=0 | |||
| i.e., x\epsilon | +ve | i.e., -ve |
Now putting the signs on real axis for each interval and value of x, we get
\therefore the domain of the function f=\sqrt} is D = [2,3)
What Is The Domain And Range Of A Square Root Function

The domain of a radical function is any x value for which the radicand is not negative. That means x + 5 0, so x 5. Since the square root must always be positive or 0,. The domain is all real numbers x where x 5, and the range is all real numbers f such that f 2.
Also Check: How To Transfer Squarespace Domain To Godaddy
What Are The Brackets For Domain And Range
4.3/5The Mathematical notation , denotes the domain of an interval.
- The brackets means: The number is included, This side of the interval is closed,
- The parenthesis means: The number is excluded, This side of the interval is open.
Moreover, what do the different brackets mean in domain and range?
Explanation: Use a bracket to indicate that the endpoint is included in the interval, a parenthesis to indicate that it is not. They always take parentheses. Quick examples: Domain of f=x is [0,)
Also Know, what is the range of the function? Range. The range of a function is the complete set of all possible resulting values of the dependent variable , after we have substituted the domain. In plain English, the definition means: The range is the resulting y-values we get after substituting all the possible x-values.
Correspondingly, how do I find the domain and range of a function?
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
How do you write a range?
Overall, the steps for algebraically finding the range of a function are:
Related Questions And Answers
How do I find the range of a function?
How do you tell if a graph is a function?
What are the examples of domain?
What is a domain in math?
How do you find range and mode?
What is difference between domain and range?
What is mean mode and range?
How do you write a range?
What if there is no mode?
How do you find the range of a quadratic function?
How do you find the range of a function in class 11?
What is the range for a straight line?
What is the standard form of a quadratic function?
How do you find the domain of a straight line?
Read Also: Who Owns Domain Name Checker
Finding The Domain Of A Function
More Domain And Range Examples
In case you missed it earlier, you can see more examples of domain and range in the section Inverse Trigonometric Functions.
We fire a ball up in the air and find the height h, in metres, as a function of timet, in seconds, is given by
h = 20t 4.9t2
Find the domain and range for the functionh.
Answer
Generally, negative values of time do not have any meaning. Also, we need to assume the projectile hits the ground and then stops – it does not go underground.
So we need to calculate when it is going to hit the ground. This will be when h = 0. So we solve:
20t 4.9t2 = 0
Recommended Reading: Cost Of A Domain Name Per Year
How Do You Find The Range Of A Quadratic Function
A
To find the range of a standard quadratic function in the form \=ax^2+bx+c\), find the vertex of the parabola and determine if the parabola opens up or down. To find the vertex of a quadratic in this form, use the formula \. This will give you the x-coordinate of the vertex, and the y-coordinate can be found by plugging this x-value into the original equation and solving for f . Next, determine if the parabola opens up or down. If the value of a is positive, then the parabola opens up and the range is . If the value of a is negative, then the parabola opens down and the range is . Ex. What is the range of \?
Therefore, the range of \ is .
Example: Finding The Domain Of A Function Involving A Denominator
Find the domain of the function f\left=\dfrac.
When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for x.
\begin2-x& =0 \\ -x& =-2 \\ x& =2 \end
Now, we will exclude 2 from the domain. The answers are all real numbers where x< 2 or x> 2. We can use a symbol known as the union, \cup , to combine the two sets. In interval notation, we write the solution: \left\cup \left.
In interval form, the domain of f is \left\cup \left.
Watch the following video to see more examples of how to find the domain of a rational function .
Read Also: How To Transfer Squarespace Domain To Godaddy
Domain And Range Of A Relation
November 20, 2020 by Veerendra
Before learning about Domain and Range of a Relation firstly know what Relations are. A relation is a rule that relates an element from one set to the other set. Consider two non-empty sets A and B then the relation is a subset of Cartesian Product AxB.
The domain is the set of all first elements of the ordered pairs. The range on the other hand is the set of all second elements of the ordered pairs. However, Range includes only the elements used by the function. There lies in a trick in the range i.e. Set B can be equal to the range of relation or bigger than that. This is because there can be elements in Set B that arent related to Set A.
Domain And Range Of A Function Explanation & Examples
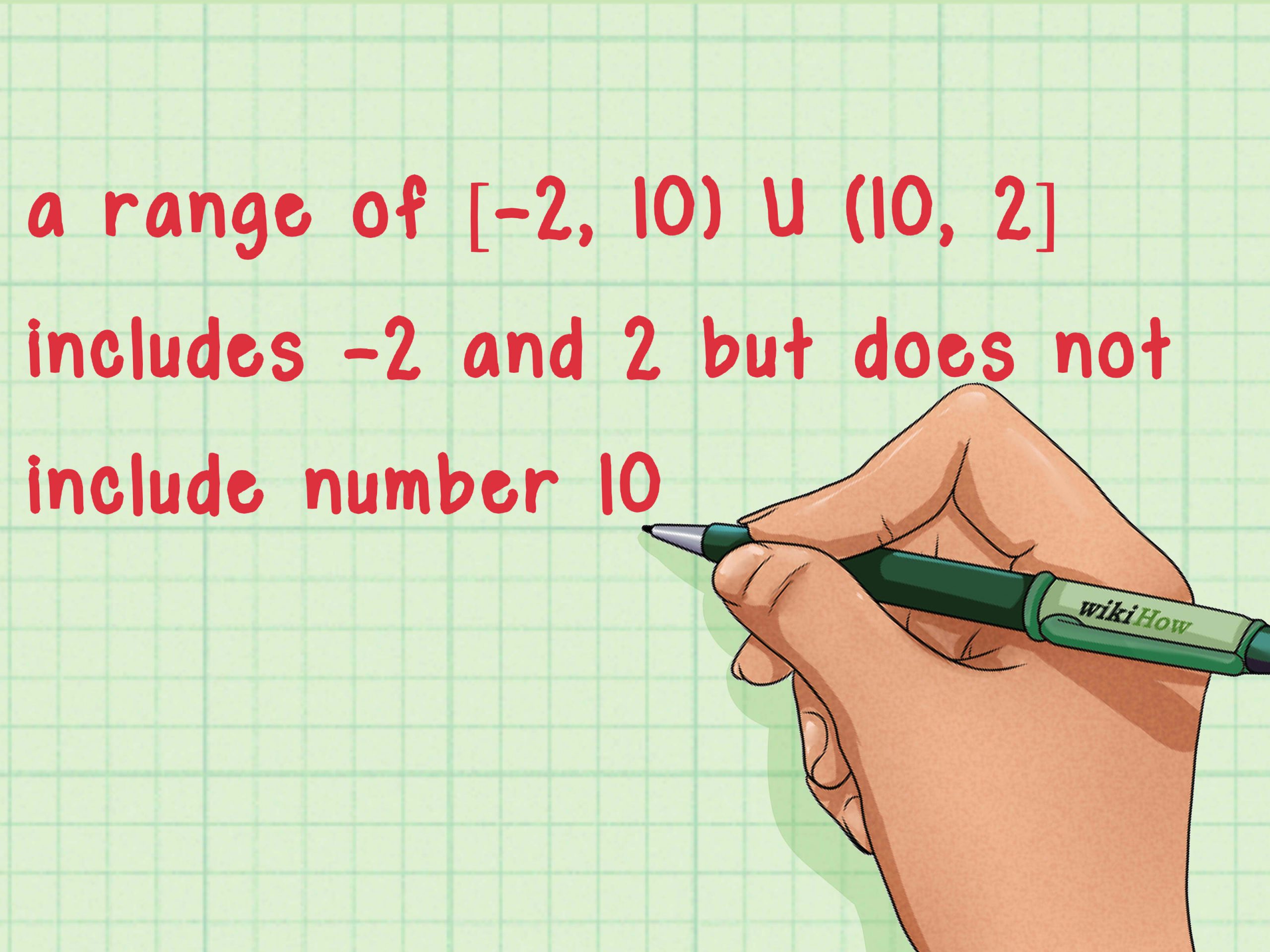
This article will explain the domain and range of a function mean and how to calculate the two quantities. Before getting into the topic of domain and range, lets briefly describe what a function is.
In mathematics, we can compare a function to a machine that generates some output in correlation to a given input. By taking an example of a coin stamping machine, we can illustrate a functions meaning as follows.
When you insert a coin into the coin stamping machine, the result is a stamped and flattened piece of metal. By considering a function, we can relate the coin and the flattened piece of metal with the domain and range. In this case, a function is considered to be the coin stamping machine.
Just like the coin stamping machine, which can only produce a single flattened piece of metal at a time, a function works in the same manner by giving out one result at a time.
Read Also: What Is The Io Domain Used For
Domain And Range Of Rational Functions
The domain of a f x is the set of all values for which the function is defined, and the range of the function is the set of all values that f
A rational function is a function of the form f
The domain of a rational function consists of all the real numbers x except those for which the denominator is 0 . To find these x values to be excluded from the domain of a rational function, equate the denominator to zero and solve for x
For example, the domain of the f is the set of all real numbers except x . Or the domain of the function f is the set of all real numbers except x
it becomes a linear function f . But the original function is not defined at x . This leaves the graph with a hole when x 2 .
One way of finding the range of a rational function is by finding the domain of the inverse function.
Another way is to sketch the graph and identify the range.
Let us again consider the parent function f . We know that the function is not defined when x
from either side of zero, f
tends to positive or negative infinity, but never touches the x -axis. That is, the function can take all the real values except 0
So, the range of the function is the set of real numbers except 0
Find the domain and range of the function y 5 .
To find the excluded value in the domain of the function, equate the denominator to zero and solve for x
So, the domain of the function is set of real numbers except 3 .
Interchange the
So, the inverse function is f 3 .
Find the domain and range of the function y .