More Domain And Range Examples
In case you missed it earlier, you can see more examples of domain and range in the section Inverse Trigonometric Functions.
We fire a ball up in the air and find the height h, in metres, as a function of timet, in seconds, is given by
h = 20t 4.9t2
Find the domain and range for the functionh.
Answer
Generally, negative values of time do not have any meaning. Also, we need to assume the projectile hits the ground and then stops – it does not go underground.
So we need to calculate when it is going to hit the ground. This will be when h = 0. So we solve:
20t 4.9t2 = 0
How To Find The Domain And Range Of A Function
We can determine the domain of a function either algebraically or by the graphical method. To calculate the domain of a function algebraically, you solve the equation to determine the values of x.
Different types of functions have their own methods of determining their domain.
Lets examine these types of functions and how to calculate their domain.
\displaystyle F = \sqrt +4
Set the radicand greater than or equal to zero and solve for x to find the restrictions on the domain:
\displaystyle \geq 0
Therefore x \geq 3. So, all real number greater than or equal to 3 is the domain of the function.
Radical function: The graph of the equation: f = \sqrt +4. The function has the domain of all real numbers greater than or equal to 3, as shown in the graph above.
Also Check: How To Transfer Google Domain To Squarespace
Domain And Range Of A Square Root Function
The function y= is defined only for x -b/a
So, the domain of the square root function is the set of all real numbers greater than or equal to b/a. We know that the square root of something always results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. The domain and range of a square root function are given as: Domain = [-b/a,), Range = [0,)
Example: y= 2-
Domain: A square root function is defined only when the value inside it is a non-negative number. So for a domain,
-3x+2 0
Range: We already know that the square root function results in a non-negative value always.
0
Multiply -1 on both sides
– 0
Adding 2 on both sides
2- 2
y 2
Importance And Use Of Frequency Domain Analysis
The term first made its appearance in 1953, in communications engineering. Today, though, this analysis is used in many different fields, including:
- Geology,
- Electrical engineering,
- Communications.
Frequency domain analysis has been called a cornerstone of systems engineering, and is an important part of the toolbox of almost any scientist, engineer or statistician.
This representation often allows us to characterize a signal or series of signals using simple algebra, as opposed to the complicated differential equations that go with a time-domain representation of a signal. The easy calculations involved with manipulating these signals make it especially useful for engineers. Perhaps more importantly, a frequency based analysis allows you to see cyclic behavior that might not have been immediately obvious in a time domain representation.
Generally speaking, an interval domain is a domain restricted to an interval . For example, inputs for a particular function might be restricted to the interval . Intervals can be closed, open, or half-closed/half-open.
A function defined on the half open interval interval domain of [5.5, 10).
Also Check: How Much Does A Domain Name Cost
Domain And Range: Other References
Cassidy, Steve. COMP449 Course Notes. Speech Recognition: Chapter 6. Frequency Dom. Analysis. Retrieved from http://web.science.mq.edu.au/~cassidy/comp449/html/ch06.html on June 15, 2018Kulkarni. Frequency Dom. and Fourier Transforms. Retrieved from https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf on June 16, 2018.Liu, G. Calculus of Several Variables. Retrieved August 31, 2020 from: https://www.math.ucla.edu/~azhou/teaching/18W/hw-solutions.pdfMIT Department of Mechanical Engineering. 2.14 Handout Introduction to Freq. Domain Processing. Retrieved from http://web.mit.edu/2.14/www/Handouts/FreqDom.pdf on June 16, 2018.Qi, P. . Answering Complex Open-domain Questions at Scale. Retrieved January 7, 2020 from: http://ai.stanford.edu/blog/answering-complex-questions/Rogawski, J.. Multivariable Calculus. W. H. Freeman.
Finding Domain And Range Without Using A Graph
It’s always a lot easier to work out the domain and range when reading it off the graph . However, we don’t always have access to graphing software, and sketching a graph usually requires knowing about discontinuities and so on first anyway.
As meantioned earlier, the key things to check for are:
Recommended Reading: How Much Does It Cost To Buy A Web Domain
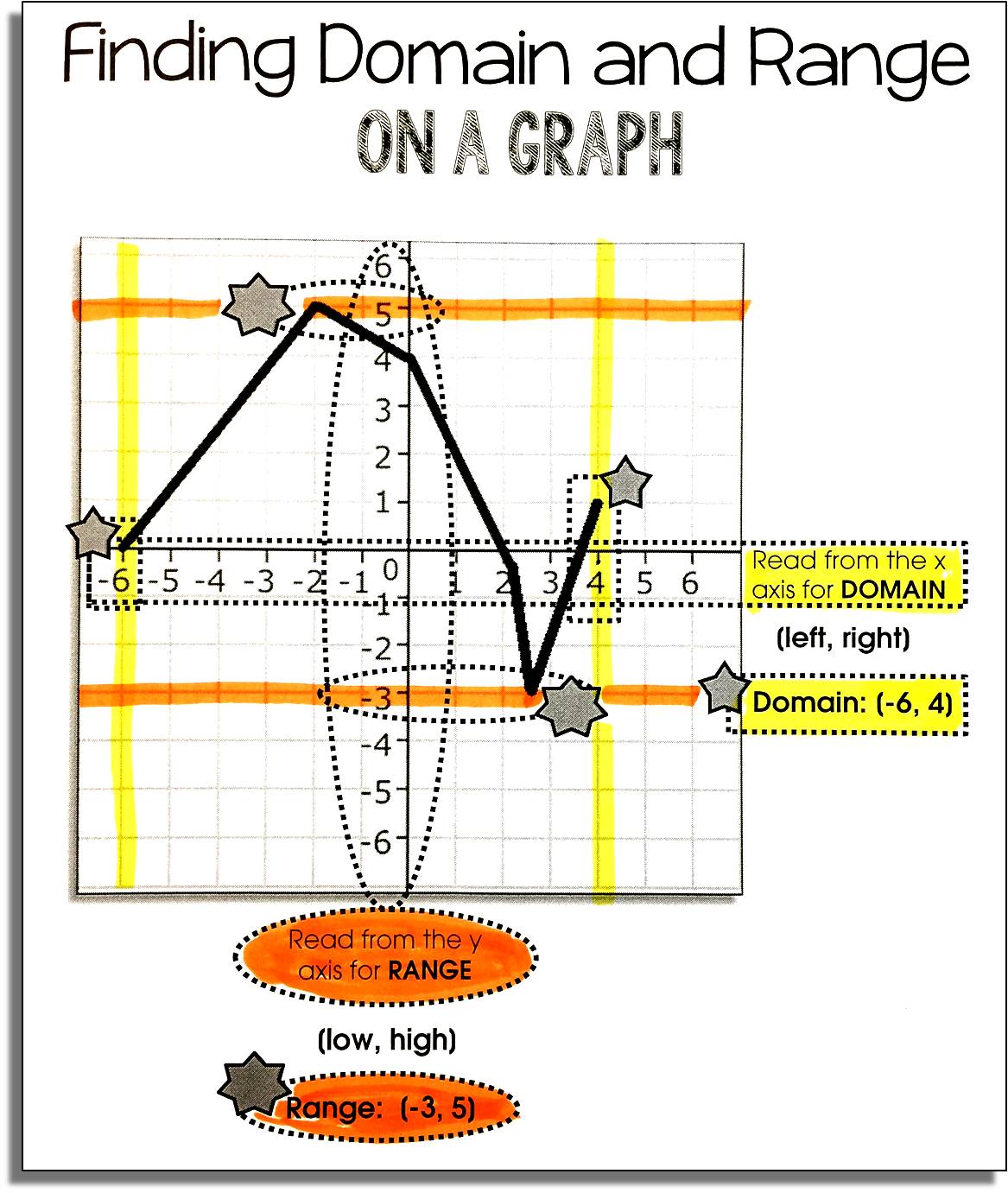
Find The Domain And Range From Graphs
We know that the domain of a function is the set of all input values. So, the domain on a graph is all the input values shown on the \-axis. To find the domain, we need to analyse how the graph looks like horizontally. Moving from left to right along the \-axis, identify the span of values for which the function is defined.
Similarly, the range of a function is the set of all output values. On a graph, this is identified as the values that are taken by the dependent variable \. So, to find the range, look at the set of values that the graph spreads vertically.
Consider the graph of the function \.
Looking at the horizontal and vertical spread of the graph, the domain, and the range can be calculated as shown below.
The closed points on either end of the graph indicate that they are also part of the graph. Therefore, the domain is \ and the range is \.
Now, if you have open points instead, the function is not defined at that point.
Here, the domain is \ and the range is \. Note that, here the value \ is included in the range as it already has a pre-image at \ and \
Sometimes the graph continues beyond the portion shown. In such cases, the domain and range could be greater than the visible values.
Generally, the arrows on either end show that the graph extends infinitely in both directions, and hence, the domain is the set of all real numbers. However, the range in this particular case remains the same as \
How To Find The Range Of A Function
The range is the set of images of the elements in the domain.
To find the range of a function:
Step 1: Write down the function in the form \\)
Step 2: Solve it for \ to write it in the form, \\)
Step 3: The domain of the function \\) is the range of \\).
Example: For the function \=\log x\), the image takes up the values from \ to \. That is, the range of the function is the set of all real numbers.
You May Like: Get A Io Domain
Finding The Domain Of A Function Defined By An Equation
In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a holding area that contains raw materials for a function machine and the range as another holding area for the machines products. See .
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has ?100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and writeWe will discuss interval notation in greater detail later.
Before we begin, let us review the conventions of interval notation:
Check For Known Domains/ranges
See if you can figure out what type of function you have first .
Many functions have an infinite set for the domain. An infinite set is just the set of all possible numbers. For example, you could input any number you like into the function y = x2, and it will still give you an output. But what about the range? A negative number will never show for this function a negative times a negative will always be positive. If you put, for example, -10 in, you get:y = -102 = -10 * -10 = 100.It makes sense that the range for x2 is 0 > .
Certain functions have defined domains and range. A brief summary is below, or check out our playlist on YouTube which has a series of very short videos on finding domains and ranges for a variety of functions.
Tip: Become familiar with the shapes of basic functions like sin/cosine and polynomials. That way, youll be able to reasonably find the domain and range of a function just by looking at the equation.
Don’t Miss: How Much For A Domain
How To The Domain For A Function With A Variable Inside A Radical Sign
To find the domain of the function, the terms inside the radical are set the inequality of > 0 or 0. Then, the value of the variable is determined.
Lets see a few examples below to understand this scenario.
Example 6
Find the domain of f =
Solution
To avoid the square roots of negative numbers, we set the expression inside the radical sign to 0.
6 + x x2 0 x 2 x 6 0
x 2 x 6= = 0
Therefore, the function is zero if x = 3 or x = -2
Hence the domain:
Example 7
Find the domain of f =x/
Solution
Set the expression within the radical sign to x2 9 > 0Solve for the variable to get
x = 3 or 3
Find the domain of f = 1/
Solution
Test your answer by plugging -3 into the expression within the radical sign.
2 4 = 5
02 4 = -4, therefore number between 2 and -2 are invalid
Try number above 2
32 4 = 5. This one is valid.
Hence, the domain = U
Using Notations To Specify Domain And Range
In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation. For example, \ describes the behavior of x in set-builder notation. The braces \ are read as the set of, and the vertical bar \ is read as such that, so we would read\ as the set of x-values such that 10 is less than or equal to x, and x is less than 30.
Figure \ compares inequality notation, set-builder notation, and interval notation.
To combine two intervals using inequality notation or set-builder notation, we use the word or. As we saw in earlier examples, we use the union symbol, \,to combine two unconnected intervals. For example, the union of the sets\ and \ is the set \. It is the set of all elements that belong to one or the other of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is
\\cup\left
Set-Builder Notation and Interval Notation
\ \nonumber\]
Given a line graph, describe the set of values using interval notation.
Solution
You May Like: How To Transfer A Domain From Squarespace
The Importance Of Codomain
Let me ask you a question: Is square root a function?
If we say the codomain is the set of real numbers, then square root is not a function! … is that a surprise?
The reason is that there could be two answers for one input, for example f = 3 or -3
A function must be single valued. It cannot give back 2 or more results for the same input. So “f = 3 or -3″ is not right!
But it can be fixed by simply limiting the codomain to non-negative real numbers.
In fact, the radical symbol always means the principal square root, so x is a function because its codomain is correct.
So, what we choose for the codomain can actually affect whether something is a function or not.
What Is A Codomain
A codomain contains all values of a function.
When we say that a function f: X Y, the codomain is the Y. In other words, the output from a function is constrained to the codomain.
The range is similar, but the difference is that a range is the set of the actual values of the function . A codomain or target set can contain every possible output, not just those that actually appear. For example, you might specify that a codomain is the set of all real numbers . However, that doesnt mean that all real numbers are outputs for your function.
Don’t Miss: How Much Do Domains Cost Per Year
What Is The Domain Codomain And Range Of A Function
The set of elements in \ that are plugged into the function \ is called the domain.
The set \ that is a collection of possible outcomes is called the codomain. The set of images of the elements in \, which is a subset of \ is called the range of the function \
Range \
For the function \
Domain \
Codomain \
Range \
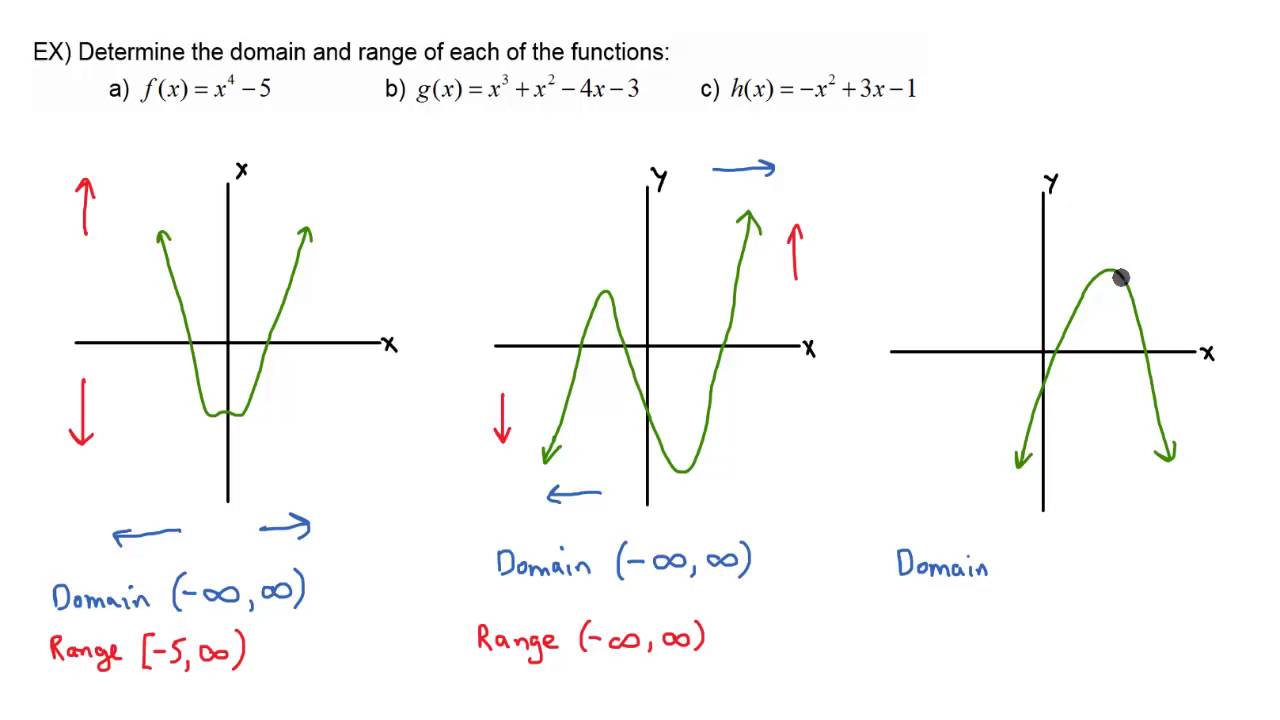
Finding Domains And Ranges Of The Toolkit Functions
We will now return to our set of toolkit functions to determine the domain and range of each.
For the constant function\=c\), the domain consists of all real numbers there are no restrictions on the input. The only output value is the constant \, so the range is the set \ that contains this single element. In interval notation, this is written as \, the interval that both begins and ends with \.
Figure \: Identity function f=x.
For the identity function \=x\), there is no restriction on \. Both the domain and range are the set of all real numbers.
For the absolute value function \=|x|\), there is no restriction on \. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
For the quadratic function \=x^2\), the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.
For the cubic function \=x^3\), the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.
Figure \: Square root function \=\sqrt\).
For the cube root function \=\sqrt\), the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative .
Read Also: Shopify Transferring Domain