Interval Domain In Domain Theory
In domain theory, the term interval domain, first proposed by D.S. Scott in 1972 , is a way to approximate real numbers. It gets its name because the reals are divided into intervals for calculations.
Approximations are sometimes needed for calculations over uncountable spaces, such as the Reals or some function spaces. Interval domains are not as straightforward to define as the intervals you come across in calculus Algebraic structures, which consist of a set plus one or more binary operations that to satisfy certain axioms, are needed to show the differences between the many equivalent versions of interval domain .
Scotts domain-theoretic framework for differential calculus was originally designed for single variable functions. It has more recently been extended to functions of several variables . This extension carries the interval domain to approximations of curves and surfaces .
Domain theory and algebraic structures are beyond the scope of this article, but if youre interested then read Jess Blancks Computer Journal article Interval Domains and Computable Sequences: A Case Study of Domain Reductions .
Domain And Range Of The Graph Of The Parabola
Example
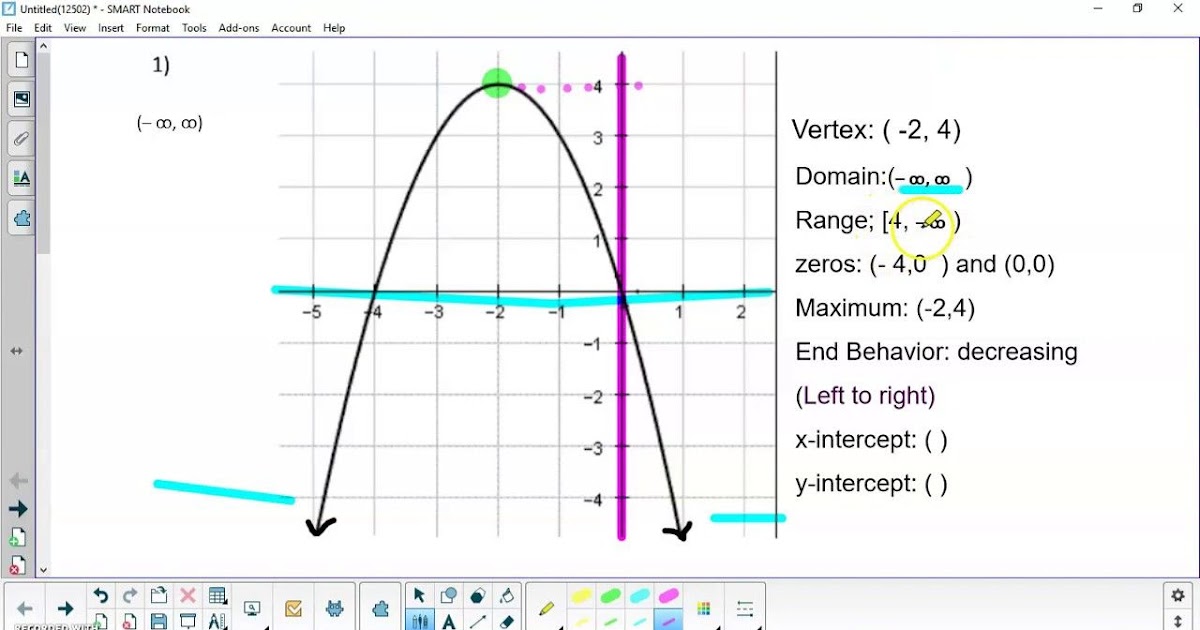
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Lets start with the domain. Remember that domain is how far the graph goes from left to right.
Start by looking at the farthest to the left this graph goes. The ???x???-value at the farthest left point is at ???x=-2???. Now continue tracing the graph until you get to the point that is the farthest to the right. The ???x???-value at this point is at ???2???. There are no breaks in the graph going from left to right which means its continuous from ???-2??? to ???2???.
Domain: ?????? also written as ???-2\leq x\leq 2???
Next, lets look at the range. Remember that the range is how far the graph goes from down to up.
Look at the furthest point down on the graph or the bottom of the graph. The ???y???-value at this point is ???y=1???. Now look at how far up the graph goes or the top of the graph. This is when ???x=-2??? or ???x=2???, but now were finding the range so we need to look at the ???y???-value of this point which is at ???y=5???. There are no breaks in the graph going from top to bottom which means its continuous.
Range: ?????? also written as ???1\leq y\leq 5???
Lets try another example of finding domain and range from a graph.
Remember that The domain is all the defined x-values, from the left to right side of the graph.
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
The Attempt At A Solution
- 801
- 1
chetzread said:negative number are ok , as long as x+y > 0 , so , Can i write the domain as ?
Hi Chetzread,You may be a little confused because typically we see the equation y = f.My advice is to reword the equation to z = f = f, where u = x + ySo ask yourself what is the domain of f? What values can u take? What values of x and y add to give u?You are correct, both x and y cannot be equal to 0 at the same time. However, you may be surprised to learn that either x and y can be negative .Below is a plot of z = ln , where x is the horizontal axis, y is the axis going out of the page, and z is the vertical axis. Note what we have discussed about the cases y< 0, x< 0, x=0, y=0.https://www4b.wolframalpha.com/Calculate/MSP/MSP37851g488iahb1eeddb60000639baefd52h542g2?MSPStoreType=image/gif& s=63
chetzread said:so , if i write the limit as ## \neq ## and ##x+y> 0## at the same time , then , my ans would be correct ?How if i write the domain as ##x+y> 0## only , without ## \neq ## , is it correct ?
chetzread said:so , if i write the limit as ## \neq ## and ##x+y> 0## at the same time , then , my ans would be correct ?How if i write the domain as ##x+y> 0## only , without ## \neq ## , is it correct ?
or
chetzread said:ok , i have one more question here , for the domain of ln , it it given in my notes that the ans is x 0 , y 0IMO , there ‘s no need to give x 0 , y 0 , so just leave the ans > 0 , will do ?
chetzread said:what do you mean ?
Read Also: How Do I See Who Owns A Domain
Finding The Domain And Range Of A Function: Overview Method Examples
Finding the Domain and Range of a Function: Domain, in mathematics, is referred to as a whole set of imaginable values. These values are independent variables. In other words, in a domain, we have all the possible x-values that will make the function work and will produce real y-values. The range, on the other hand, is set as the whole set of possible yielding values of the depending variable, which in this case, is y .
Finding the domain requires determining the values of the independent variables that have been allowed to use. At the bottom of the fraction, 0 is usually debarred or we generally avoid negative values that are found under the square root sign. The range of a function is considered as an array of possible y-values. Continue reading to learn more about the domain and range of a function.
What Is A Codomain
A codomain contains all values of a function.
When we say that a function f: X Y, the codomain is the Y. In other words, the output from a function is constrained to the codomain.
The range is similar, but the difference is that a range is the set of the actual values of the function . A codomain or target set can contain every possible output, not just those that actually appear. For example, you might specify that a codomain is the set of all real numbers . However, that doesnt mean that all real numbers are outputs for your function.
Read Also: How To Change My Website Domain Name
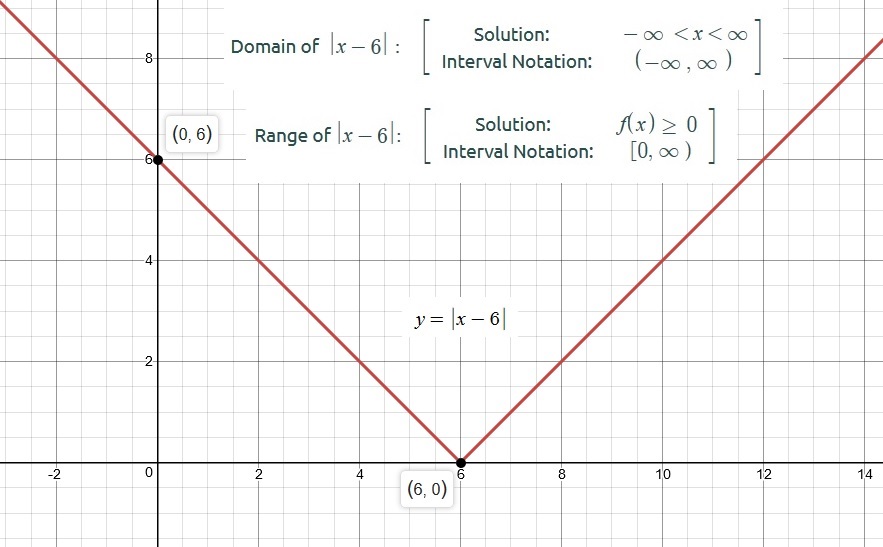
Find The Domain And Range From Graphs
We know that the domain of a function is the set of all input values. So, the domain on a graph is all the input values shown on the \-axis. To find the domain, we need to analyse what the graph looks like horizontally. Moving from left to right along the \-axis, identify the span of values for which the function is defined.
Similarly, the range of a function is the set of all output values. On a graph, this is identified as the values that are taken by the dependent variable \. So, to find the range, look at the set of values that the graph spreads vertically. Those looking for the domain and range calculator should take help from the figures shown on this page.
Consider the graph of the function \.
Looking at the horizontal and vertical spread of the graph, the domain, and the range can be calculated as shown below.
The closed points on either end of the graph indicate that they are also part of the graph. Therefore, the domain is \ and the range is \.
Now, if you have open points instead, the function is not defined at that point.
Here, the domain is \ and the range is \. Note that, here the value \ is included in the range as it already has a pre-image at \ and \
Sometimes the graph continues beyond the portion shown. In such cases, the domain and range could be greater than the visible values.
How To Find The Range Of A Function
The range is the set of images of the elements in the domain.
To find the range of a function:
- Step 1: Write down the function in the form \\)
- Step 2: Solve it for \ to write it in the form, \\)
- Step 3: The domain of the function \\) is the range of \\).
Example: For the function \=\log x\), the image takes up the values from \ to \. That is, the range of the function is the set of all real numbers.
Recommended Reading: How To Sell A Google Domain
Closed Domain In Other Contexts
In artificial intelligence, closed domain refers to a situation specific system in question answering . For example, a system called AIRPLANE might be good at answering questions about air speed, acceleration and capacity of specific aircraft, it isnt very good beyond that specific area. An open-domain QA on the other hand, is able to sift through an unlimited domain to find the answer to a question.
In software engineering, a closed domain is simply a domain where all boundaries are closed. An open domain is one where all boundaries are open.
Integrally closed domains are found in commutative algebra. An integrally closed domain A is an integral domain whose integral closure in its field of fractions is A itself.
Importance And Use Of Frequency Domain Analysis
The term first made its appearance in 1953, in communications engineering. Today, though, this analysis is used in many different fields, including:
- Electrical engineering,
- Communications.
Frequency domain analysis has been called a cornerstone of systems engineering, and is an important part of the toolbox of almost any scientist, engineer or statistician.
This representation often allows us to characterize a signal or series of signals using simple algebra, as opposed to the complicated differential equations that go with a time-domain representation of a signal. The easy calculations involved with manipulating these signals make it especially useful for engineers. Perhaps more importantly, a frequency based analysis allows you to see cyclic behavior that might not have been immediately obvious in a time domain representation.
Generally speaking, an interval domain is a domain restricted to an interval . For example, inputs for a particular function might be restricted to the interval . Intervals can be closed, open, or half-closed/half-open.
A function defined on the half open interval interval domain of [5.5, 10).
Recommended Reading: How To Find Out Domain Registrar
What Are The Rules To Find The Domain Of A Function
Here are some general rules used to find domain of different types of functions:
- f = polynomial, the domain is the set of all real numbers.
- f = 1/x, domain if the set of all real numbers but x0.
- f = x, domain if the set of all real numbers such that x 0.
- f = ln x, domain is the set of all real numbers such that x > 0.
Solved Examples On Domain And Range Of A Relation:
1. In the given ordered pair find the following relations. Also, find the domain and range. Is two less than
Is less than
Is equal to Solution: R is the set of all ordered pairs whose 1 component is two less than the 2 component.
Therefore, R =
Also, Domain = Set of all first components of R = and Range = Set of all second components of R =
R is the set of all ordered pairs whose 1 component is less than the second component.
Therefore, R = .
Also, Domain = and Range =
R is the set of all ordered pairs whose 1 component is greater than the second component.
Therefore, R =
Also, Domain = and Range =
R is the set of all ordered pairs whose 1 component is equal to the second component.
Therefore, R =
Also, Domain = and Range =
2. Let A = and B = .
Let R be the relation is factor of from A to B. Write R in the roster form. Also, find Domain and Range of R. Draw an arrow diagram to represent the relation. Solution: Clearly, R consists of elements where a is a factor of b. Therefore, Relation in the roster form is R = Therefore, Domain = Set of all first components of R = and Range = Set of all second components of R = The arrow diagram representing R is as follows:
3. The arrow diagram shows the relation from set A to set B. Write this relation in the roster form.
Solution:Clearly, R consists of elements , such that a is square of b i.e., a = b². So, in roster form R =
Read Also: How To Get A Cheap Domain Name
Domain And Range Of A Relation
In domain and range of a relation, if R be a relation from set A to set B, then The set of all first components of the ordered pairs belonging to R is called the domain of R. Thus, Dom = . The set of all second components of the ordered pairs belonging to R is called the range of R.
Thus, range of R = . Therefore, Domain = and Range =
Note:The domain of a relation from A to B is a subset of A.
The range of a relation from A to B is a subset of B.
For Example:If A = .
Let R be the relation is less than from A to B. Find Domain and Range . Solution:Under this relation , we have
Therefore, Domain = and Range =
The Importance Of Codomain
Let me ask you a question: Is square root a function?
If we say the codomain is the set of real numbers, then square root is not a function! … is that a surprise?
The reason is that there could be two answers for one input, for example f = 3 or -3
A function must be single valued. It cannot give back 2 or more results for the same input. So “f = 3 or -3″ is not right!
But it can be fixed by simply limiting the codomain to non-negative real numbers.
In fact, the radical symbol always means the principal square root, so x is a function because its codomain is correct.
So, what we choose for the codomain can actually affect whether something is a function or not.
You May Like: How To Create An Email With Your Domain Name
Functions: Domain And Range
Functions have a domain and range and can be found in two ways. If the function is graphed, the domain and range can be identified from the picture, or the domain and range can be found algebraically with some reasoning.
Domain
The domain of a function is the set of all x-values that have a y-value associated with them. In other words, it is the set of all inputs that will receive an output.
Examples
Find the domain of y = x.
The graph of y = x is shown to the right. We can see that it is defined for all x-values because the line will continue to infinity. Thus, the domain of y = x is all real numbers.
Find the domain of
We do not have the graph but there are properties of the square root function that we can use in order to determine the domain. In order to square root a number, it must be greater or equal to 0. This tells us that y only has a value when x is greater or equal to 0. Therefore the domain is x must be greater or equal to 0.
Range
The range of a function is the set of all y-values that have a corresponding x-value. In other terms, it is the set of all outputs of a function that have an input.
Example
Find the range of y = x2.
The graph y = x2 is the standard parabola as shown to the right. We can see that the graph has y-values that continue to positive infinity but have a minimum of 0 at the origin. There are no points that have a y-value less than 0 and so the range is y must be greater or equal to 0.
Finding The Domain Of A Function Defined By An Equation
In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.
We can visualize the domain as a holding area that contains raw materials for a function machine and the range as another holding area for the machines products ).
We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket \). We will discuss interval notation in greater detail later.
Before we begin, let us review the conventions of interval notation:
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- Parentheses, \ or \\), are used to signify that an endpoint is not included, called exclusive.
- Brackets, \, are used to indicate that an endpoint is included, called inclusive.
Don’t Miss: How To Change Ownership Of Domain Name