Example: Find The Domain And Range Of A Function With Algebra
Find the domain and range for:Domain:
- The numerator has a square root numbers under this cant be negative . So you can only have numbers for x greater than or equal to -2.
- The denominator: You cant have division by zero, you cant have -3 + 3 as this would result in zero. For example, 32 9 = 0.
The domain for this particular function is x > -2, x 3.
RangeThe range for this function is the set all values of f excluding F = 0. Heres where your algebra skills get a workout!
- Numerator: By looking at the function, you should immediately see that the numerator becomes 0 when x = -2: = 0 = 0.
- Denominator:
- Working with -2 still, the denominator becomes: 2 9 = 5.So f = 0/-5 = 0.
- If you insert a few x-values between 2 and 3 into , youll see that the function approaches negative infinity.
- Insert some more x-values greater than x = 3, note that the function tends toward positive infinity.
- The larger the x-values get, the smaller the function values get .
How To Use Interval Notations To Specify Domain And Range
Since the range and domain of a function are usually expressed in interval notation, its important to discuss the concept of interval notation.
The procedure for doing interval notation include:
- Write the numbers separated by a comma in ascending order.
- Enclose the numbers using parentheses to show that an endpoint value is not included.
- Use brackets to enclose the numbers when the endpoint value is included.
Domain And Range Of A Parabola
The range of a function is the set of output values when all x-values within the domain are evaluated into the function, commonly referred to as the y-values. This means I want to seek out the domain first so as to explain the range.
Finding the range of a quadratic function may be a bit more tricky than finding the domain of a quadratic function. Sometimes you can use a graphing calculator to possess an accurate picture of the function. And, if you dont want to use it, I encourage you to sketch a graph.
Either way, it’s crucial that you simply have an honest idea of how the graph seems so as to properly describe the range of the function.
You May Like: Io Domain Name Meaning
How To Find The Domain And The Range Of Exponential Functions
Recall that the domain is the set of input values that are used for the independent variable.
Also, remember that the range is the set of all the output values for the dependent variable.
For any exponential function with the general form , the domain is the set of all real numbers. That is, we have:
For any exponential function with the general form , the range is the set of all real numbers above or below the horizontal asymptote, . The range does not include the value of the asymptote, d. That is, we have:
How To Find The Domain For A Rational Function With A Variable In The Denominator
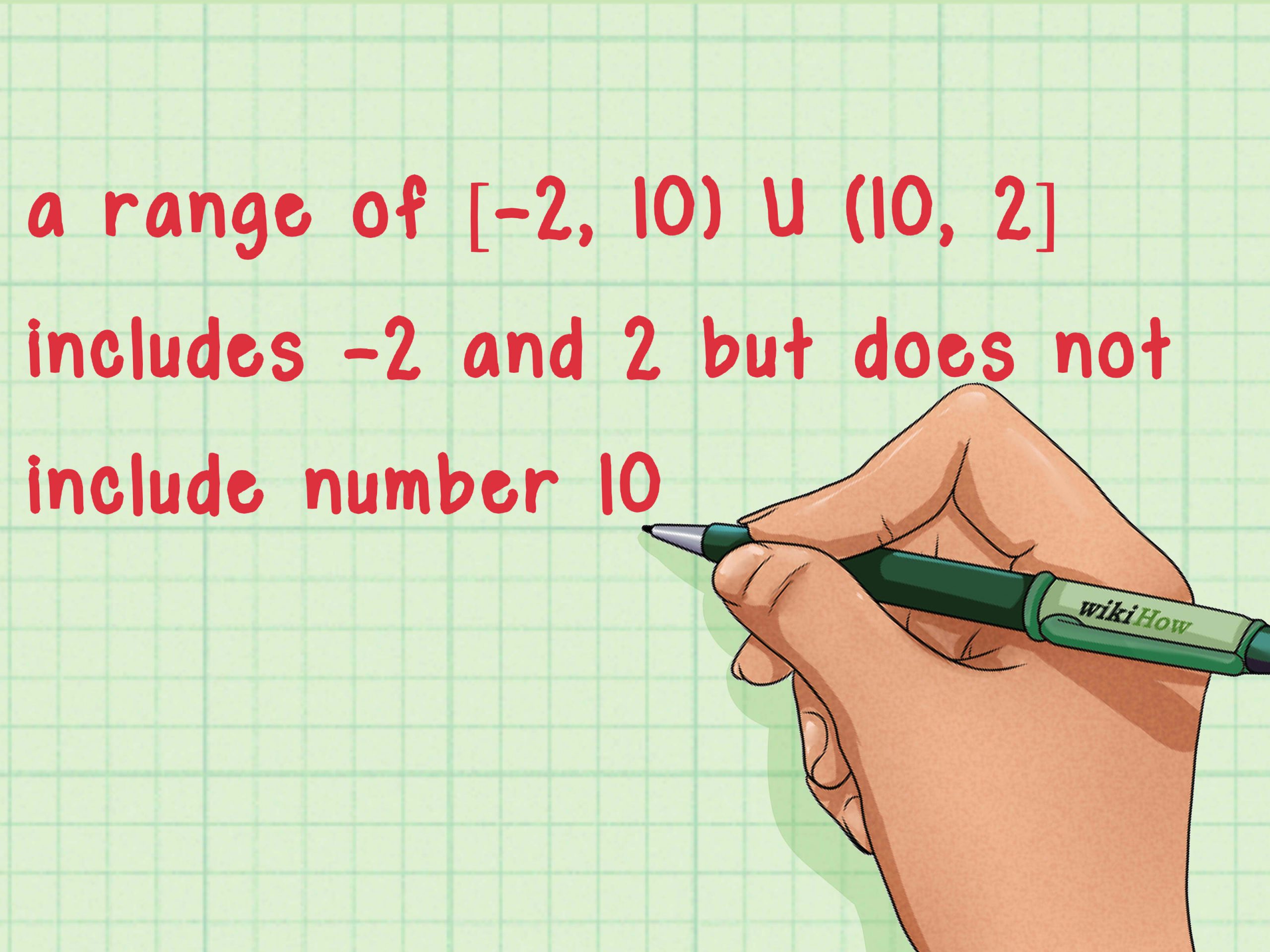
To find the domain of this type of function, set the denominator to zero and calculate the variables value.
Lets see a few examples below to understand this scenario.
Example 3
Determine the domain of x4/
Solution
Set the denominator to zero and solve for x
x2 2x 15 = = 0
Hence, x = 3, x = 5
For the denominator not to be zero, we need to avoid the numbers 3 and 5. Therefore, the domain is all real numbers except 3 and 5.
Example 4
Calculate the domain and the range of the function f = -2/x.
Solution
Set the denominator to zero.
x = 0
Therefore, domain: All real numbers except 0.
The range is all real values of x except 0.
Example 5
Find the domain and range of the following function.
f = 2/
Set the denominator equal to zero and solve for x.
x + 1 = 0
= -1
Since the function is undefined when x = -1, the domain is all real numbers except -1. Similarly, the range is all real numbers except 0
Recommended Reading: Transfer Shopify Domain To Another Host
Domain And Range Of The Graph Of The Parabola
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Lets start with the domain. Remember that domain is how far the graph goes from left to right.
Start by looking at the farthest to the left this graph goes. The ???x???-value at the farthest left point is at ???x=-2???. Now continue tracing the graph until you get to the point that is the farthest to the right. The ???x???-value at this point is at ???2???. There are no breaks in the graph going from left to right which means its continuous from ???-2??? to ???2???.
Domain: ?????? also written as ???-2\leq x\leq 2???
Next, lets look at the range. Remember that the range is how far the graph goes from down to up.
Look at the furthest point down on the graph or the bottom of the graph. The ???y???-value at this point is ???y=1???. Now look at how far up the graph goes or the top of the graph. This is when ???x=-2??? or ???x=2???, but now were finding the range so we need to look at the ???y???-value of this point which is at ???y=5???. There are no breaks in the graph going from top to bottom which means its continuous.
Range: ?????? also written as ???1\leq y\leq 5???
Lets try another example of finding domain and range from a graph.
Remember that The domain is all the defined x-values, from the left to right side of the graph.
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Examples On Domain And Range
Example 1. Find the domain and range of the real function f defined by f =
Solution: Given the function is real. Thus the domain and range of the function are also real.
| x | |
|---|---|
| = -3 | No |
Thus f is always non-negative, and the minimum value it could take is 1 and the maximum value is . Thus domain = [1, ).
The minimum value of the range is 0 and it can range up to infinity. Thus range = [0, )
Answer: The domain and the range of the function f defined by f = is domain = [1, ) and range = [0, )
Example 2: We define a function f: R-0 R as f=1/x. Complete the table shown below. Find the domain and range of the function.
| x |
|---|
Solution:
Let’s complete the given table by finding the values of the function at the given values x. Plugging in the values of x in the given function, we find the range of f = 1/x.
| x | |
|---|---|
| 2 | 0.5 |
Let’s draw the graph of the function to determine the domain and range of the function.
Answer: From the graph, we can observe that the domain and range of the function are all real numbers except 0. So, the domain and range of f=1/x is R-
Read Also: How Much Does It Cost To Own A Domain
How Many Kilometers Are In A Dollar
Additionally How do you find the domain on a calculator?
How do I find range of a function? Overall, the steps for algebraically finding the range of a function are:
What Is The Domain And Range Of Composite Functions
Let the composite function be \. The domain and range of h are determined as follows. The domain of h is either same as f or lies within the domain of f. The range h must lie within the range of g. Let f = x2 and g = x+ 3. We know that f: X Y and g: Y Z. Then fog: X Z. f) = 2. Thus the domain and range are: domain= , range=
Don’t Miss: How Much Does It Cost To Buy A Web Domain
Rules To Remember When Finding The Domain Of A Function
We should always remember the following rules when finding the domain of a function:
The 7 rules mentioned above will make our work easy when we find the domain of a function.
There are 2 other rules. We will learn them at the time of discussion.
Domain And Range Of A Function
The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and range is the possible output given by the function. Domain Function Range. If there exists a function f: A B such that every element of A is mapped to elements in B, then A is the domain and B is the co-domain. The image of an element ‘a’ under a relation R is given by ‘b’, where R. The range of the function is the set of images. The domain and range of a function is denoted in general as follows: Domain = and range=
The domain and range of this function f = 2x is given as domain D = , range R =
Also Check: Domainnamechecker
Find Domain Of A Logarithmic Function
From Rule 7 we know that a Logarithmic Function of the form f=\ln \left \right ) is defined when g> 0.
Example:
The function f= \ln is defined when
x-2> 0
Therefore f= \ln is defined for all x> 2.
\therefore domain of f= \ln is
D = :x> 2} =
Example:
f= \ln
Solution:
The function f= \ln is defined when
x^-3x+2> 0
i.e., > 0
| > 0 satisfied or not |
|---|
| x=.5< 1 |
i.e., x< 1 and x> 2
\therefore domain of the function f= \ln is
D = :x< 1,x> 2} = \cup
Importance And Use Of Frequency Domain Analysis

The term first made its appearance in 1953, in communications engineering. Today, though, this analysis is used in many different fields, including:
- Geology,
- Electrical engineering,
- Communications.
Frequency domain analysis has been called a cornerstone of systems engineering, and is an important part of the toolbox of almost any scientist, engineer or statistician.
This representation often allows us to characterize a signal or series of signals using simple algebra, as opposed to the complicated differential equations that go with a time-domain representation of a signal. The easy calculations involved with manipulating these signals make it especially useful for engineers. Perhaps more importantly, a frequency based analysis allows you to see cyclic behavior that might not have been immediately obvious in a time domain representation.
Generally speaking, an interval domain is a domain restricted to an interval . For example, inputs for a particular function might be restricted to the interval . Intervals can be closed, open, or half-closed/half-open.
A function defined on the half open interval interval domain of [5.5, 10).
You May Like: How Much Does It Cost For A Domain Name
Finding Domain And Range From Graphs
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values. See Figure \.
We can observe that the graph extends horizontally from 5 to the right without bound, so the domain is \. Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.
Example \: Finding Domain and Range from a Graph
Find the domain and range of the function f whose graph is shown in Figure 1.2.8.
Solution
We can observe that the horizontal extent of the graph is 3 to 1, so the domain of f is \.
The vertical extent of the graph is 0 to 4, so the range is \\). See Figure \.
Example \: Finding Domain and Range from a Graph of Oil Production
Find the domain and range of the function f whose graph is shown in Figure \.
Solution
In interval notation, the domain is \, and the range is about \. For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.
Exercse \
Given Figure \, identify the domain and range using interval notation.
Closed Domain In Other Contexts
In artificial intelligence, closed domain refers to a situation specific system in question answering . For example, a system called AIRPLANE might be good at answering questions about air speed, acceleration and capacity of specific aircraft, it isnt very good beyond that specific area. An open-domain QA on the other hand, is able to sift through an unlimited domain to find the answer to a question.
In software engineering, a closed domain is simply a domain where all boundaries are closed. An open domain is one where all boundaries are open.
Integrally closed domains are found in commutative algebra. An integrally closed domain A is an integral domain whose integral closure in its field of fractions is A itself.
You May Like: Find Mail Server For Domain
Domain And Range Of Logarithmic Functions
Logarithmic functions are the inverse functions of the exponential functions. This means that their domain and range are swapped. The domain of logarithmic functions is equal to all real numbers greater or less than the vertical asymptote. The range of exponential functions is always equal to all real numbers since we have no restrictions on the output values.
Here, we will learn how to determine the domain and range of logarithmic functions. In addition, we will look at some examples with the graphs of the functions to illustrate these ideas.
ALGEBRA