Finding Domain Of A Function With A Square Root In The Numerator
From Rule 5 we know that a function of the form f=\frac} is defined when g\geq 0 and h\neq 0.
Example:
f=\frac}-4}
Solution:
The function f=\frac}-4} is defined when
- x+1\geq 0
- x^-4\neq 0
i.e., \neq 0
i.e., \neq 0 and \neq 0
i.e., x\neq -2 and x\neq 2
\therefore domain of f=\frac}-4} is
:x\geq -1,x\neq 2,}
We can also express the domain of the function in interval notation.
Domain of f=\frac}-4} in interval notation is [-1,2)\cup .
Domain And Range Of Toolkit Functions
We will now return to our set of toolkit functions to determine the domain and range of each.
For the constant function f\left=c, the domain consists of all real numbers there are no restrictions on the input. The only output value is the constant c, so the range is the set \left\ that contains this single element. In interval notation, this is written as \left, the interval that both begins and ends with c.
For the identity function f\left=x, there is no restriction on x. Both the domain and range are the set of all real numbers.
For the absolute value function f\left=|x|, there is no restriction on x. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
For the quadratic function f\left=^, the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.
For the cubic function f\left=^, the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.
For the cube root function f\left=\sqrt, the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative .
How Do You Find The Domain And Range Of A Linear Graph
domain and rangegraphsdomaindomaingraphrange
To determine the domain, identify the set of all the x-coordinates on the function’s graph. To determine the range, identify the set of all y-coordinates. In addition, ask yourself what are the greatest/least x- and y-values. These values will be your boundary numbers.
Subsequently, question is, how do we find the range of a function? How to find the range
Herein, what is the range in math?
The Range The Range is the difference between the lowest and highest values. Example: In the lowest value is 3, and the highest is 9. So the range is 9 3 = 6. It is that simple!
How do you find the range?
Summary: The range of a set of data is the difference between the highest and lowest values in the set. To find the range, first order the data from least to greatest. Then subtract the smallest value from the largest value in the set.
Don’t Miss: How To Access Google Domain
Domain And Range Of A Square Root Function Using Graph
A square root function is defined as :
f = x and f is valid for only the positive values of x
Clearly the domain of this square root function is all positive values of x i.e. [0,) and range of f is also [0,) .
Now lets see the graph of a square root function :
Note : Also the graph of a reciprocal function is given as :
f = 1/x , clearly domain is all R except 0 and range is also R
Finding The Domain Of A Function Using A Relation
Recommended Reading: How To Buy A Org Domain
How To Find The Domain And Range Of A Function Algebraically
Let the function be y=f. Let us find the domain and range of this function algebraically.
To calculate the domain of the function, we simply solve the equation to determine the values of the independent variable x. To calculate the range of the function, we simply express x as x = g and then find the domain of g.
How Do You Find The Range Of A Point
rangerange
Overall, the steps for algebraically finding the range of a function are:
Subsequently, question is, how do you find the domain and range of a function? Example 1:
In this regard, how do you find the range of a domain?
Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
What is a function in algebra?
A function is an equation that has only one answer for y for every x. A function assigns exactly one output to each input of a specified type. It is common to name a function either f or g instead of y. f means that we should find the value of our function when x equals 2. Example.
Recommended Reading: How Do You Obtain A Domain Name
Finding Domains And Ranges Of The Toolkit Functions
We will now return to our set of toolkit functions to determine the domain and range of each.
For the constant function\=c\), the domain consists of all real numbers there are no restrictions on the input. The only output value is the constant \, so the range is the set \ that contains this single element. In interval notation, this is written as \, the interval that both begins and ends with \.
Figure \: Identity function f=x.
For the identity function \=x\), there is no restriction on \. Both the domain and range are the set of all real numbers.
For the absolute value function \=|x|\), there is no restriction on \. However, because absolute value is defined as a distance from 0, the output can only be greater than or equal to 0.
For the quadratic function \=x^2\), the domain is all real numbers since the horizontal extent of the graph is the whole real number line. Because the graph does not include any negative values for the range, the range is only nonnegative real numbers.
For the cubic function \=x^3\), the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.
Figure \: Square root function \=\sqrt\).
For the cube root function \=\sqrt\), the domain and range include all real numbers. Note that there is no problem taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative .
Structure Of A Function
The structure of a function determines its domain and range. Some functions, such as linear functions =2x+1\)), have domains and ranges of all real numbers because any number can be input and a unique output can always be produced. On the other hand, functions with restrictions such as fractions or square roots may have limited domains and ranges =\frac\) \ because the denominator of a fraction cannot be 0).
Lets see how the structure of quadratic functions defines and helps us determine their domains and ranges.
Heres the graph of \=x^\).
Quadratic functions together can be called a family, and this particular function the parent, because this is the most basic quadratic function . We can use this function to begin generalizing domains and ranges of quadratic functions.
To determine the domain and range of any function on a graph, the general idea is to assume that they are both real numbers, then look for places where no values exist.
Read Also: Does It Cost To Have A Domain Name
Domain And Range Of The Graph Of The Parabola
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
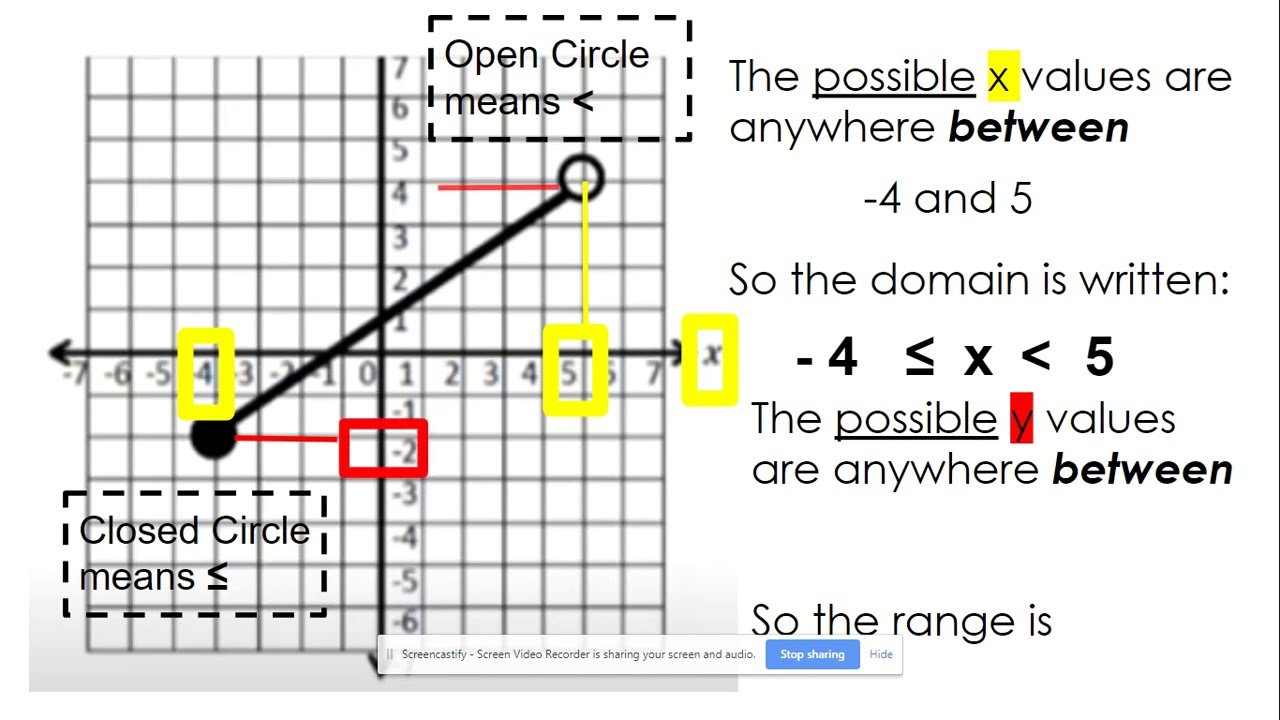
Lets start with the domain. Remember that domain is how far the graph goes from left to right.
Start by looking at the farthest to the left this graph goes. The ???x???-value at the farthest left point is at ???x=-2???. Now continue tracing the graph until you get to the point that is the farthest to the right. The ???x???-value at this point is at ???2???. There are no breaks in the graph going from left to right which means its continuous from ???-2??? to ???2???.
Domain: ?????? also written as ???-2\leq x\leq 2???
Next, lets look at the range. Remember that the range is how far the graph goes from down to up.
Look at the furthest point down on the graph or the bottom of the graph. The ???y???-value at this point is ???y=1???. Now look at how far up the graph goes or the top of the graph. This is when ???x=-2??? or ???x=2???, but now were finding the range so we need to look at the ???y???-value of this point which is at ???y=5???. There are no breaks in the graph going from top to bottom which means its continuous.
Range: ?????? also written as ???1\leq y\leq 5???
Lets try another example of finding domain and range from a graph.
Remember that The domain is all the defined x-values, from the left to right side of the graph.
Example
What is the domain and range of the function? Assume the graph does not extend beyond the graph shown.
Identify The Domain And Range Of Each Relation
Finding Domain And Range Worksheet : Functions Finding Range Given Domain Worksheet By Algebra Funsheets –. Domain and range worksheet #1. Domain and range teacher resources. Then find the domain and range in set builder notation. Identify the domain and range of each relation. Worksheet by kuta software llc.
Then find the domain and range in set builder notation. Find domain and range lesson plans and worksheets. Walk through this collection of free printable worksheets and identify the domain and range of the functions from the graphs.
Domain, how do you find its value in the range? Finding domain and range of graphs worksheets teaching resources · domain insert clever math pun here · solved a 124 2 2 increasing decreasing max . Because the domain refers to the set of possible input values, the domain of a .
Then find the domain and range in set builder notation. Find the domain and range for each set of ordered pairs. Walk through this collection of free printable worksheets and identify the domain and range of the functions from the graphs.
Because the domain refers to the set of possible input values, the domain of a . Finding domain and range of graphs worksheets teaching resources · domain insert clever math pun here · solved a 124 2 2 increasing decreasing max . Identify the domain and range of each relation.
Recommended Reading: Where To Buy Co Domains
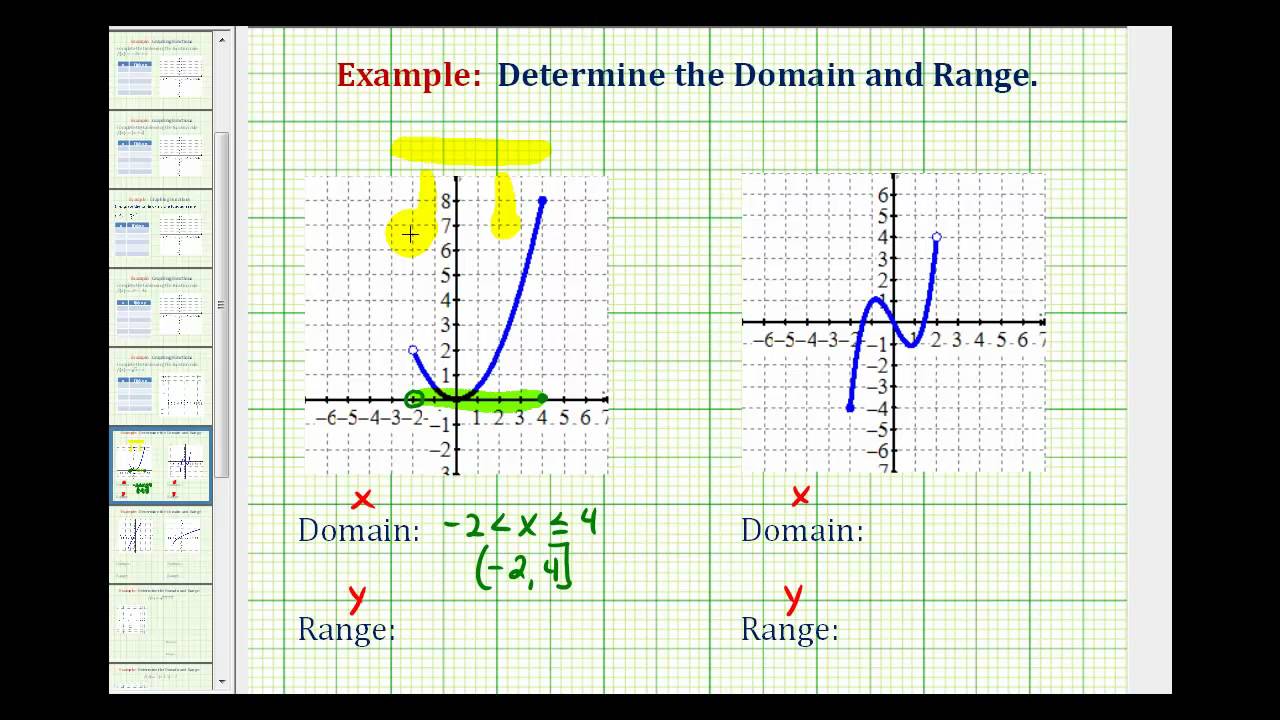
Finding The Domain Of A Function Using A Graph
Finding Domain Of A Function With A Square Root
Example:
f=\sqrt
Solution:
From Rule 3 we know that a function of the form f=\sqrt is defined when g\geq 0
i.e.,
f=\sqrt is defined when
x+2\geq 0
Putting this result on real line we get
\therefore domain of f=\sqrt is
D=: x\geq -2}=[-2,\infty ).
Example:
Find the domain of the function
f=\sqrt+3x+2}
Solution:
For f to be defined,
i.e., \geq 0
i.e., either x+2\leq 0 or x+1\geq 0
i.e., either x\leq -2 or x\geq -1
Why we write x\leq -2 and x\geq -1?
See the table given below to understand this
| Value of x | Sign of | \geq 0 satisfied or not | |
|---|---|---|---|
| x=-3 | |||
| i.e., x\epsilon | +ve | i.e., +ve |
From the table we can see that the relation \geq 0 is satisfied when
x\epsilon , x=-2, and x=-1, x\epsilon
i.e., x\epsilon
i.e., x\epsilon
\therefore domain of f=\sqrt+3x+2} is
D = \: x \: \epsilon \:
\: \: \: \: \: \: \: \: \: \: = :x\leq -2,x\geq -1}
Recommended Reading: How To Find A Website Domain
Domain And Range Of Exponential Functions
The function y = ax, a 0 is defined for all real numbers. Hence, the domain of the exponential function is the entire real line. The exponential function always results in a positive value. Thus, the range of the exponential function is of the form y= |ax+b| is y R , . Domain = R, Range =
Example: Look at the graph of this function f: 2x
Observe that the value of the function is closer to 0 as x tends to but it will never attain the value 0. The domain and range of an exponential function are given as follows:
- Domain: The domain of the function is the set R.
- Range: The exponential function always results in positive real values.